Principal Component Analysis | Dimension Reduction
Dimension Reduction Techniques- The two popular and well-known dimension reduction techniques are-
In this article, we will discuss about
Principal Component Analysis Dimension Reduction: It is defined as a process of converting a data set having vast dimensions into a data set with lesser dimensions. It ensures that the converted data set conveys similar information concisely.
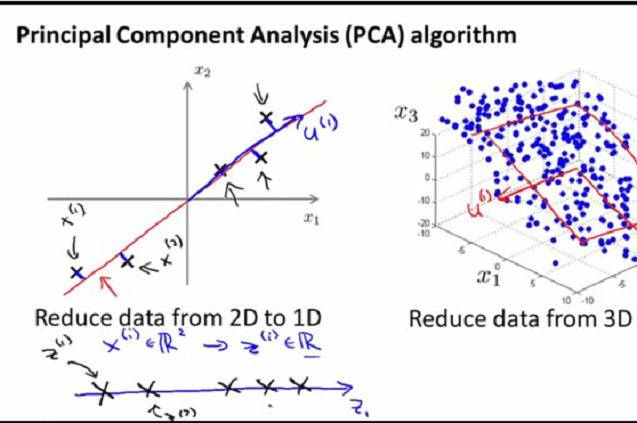
Using dimension reduction techniques in the figure example 1, we convert the dimensions of data from 2 dimensions (x1 and x2) to 1 dimension (z1). In machine learning, using both these dimensions convey similar information. Also, they introduce a lot of noise in the system. So, it is better to use just one dimension. It makes the data relatively easier to explain.
Dimension reduction offers several benefits such as:
- Compresses the data and thus reduces the storage space requirements
- Reduces the time required for computation since less dimensions require less computation
- Eliminates the redundant features
- Improves the model performance
Properties of Principal Component Analysis:
- Principal Component Analysis is a well-known dimension reduction technique
- It transforms the variables into a new set of variables called as principal components
- These principal components are linear combination of original variables and are orthogonal
- The first principal component accounts for most of the possible variation of original data
- The second principal component does its best to capture the variance in the data
- There can be only two principal components for a two-dimensional data set
PCA Algorithm- The steps involved in PCA Algorithm are as follows:
Step-01: Get data
Step-02: Compute the mean vector (µ)
Step-03: Subtract mean from the given data
Step-04: Calculate the covariance matrix
Step-05: Calculate the eigen vectors and eigen values of the covariance matrix
Step-06: Choosing components and forming a feature vector
Step-07: Deriving the new data set
Applications of Principal Component Analysis:
PCA is predominantly used as a dimensionality reduction technique in domains like facial recognition, computer vision and image compression. It is also used for finding patterns in data of high dimension in the field of finance, data mining, bioinformatics, , etc.
Some of the Chemical Engineering Software which uses PCA are Aspen ProMV, Aspen Inferential Qualities etc.



